For my programming project, I chose to revisit a game
I had played with before this class called Quantum
Game. I’ll be showing my attempts to model qubits
in this game.
Quantum Game
http://play.quantumgame.io
https://quantumgame.io
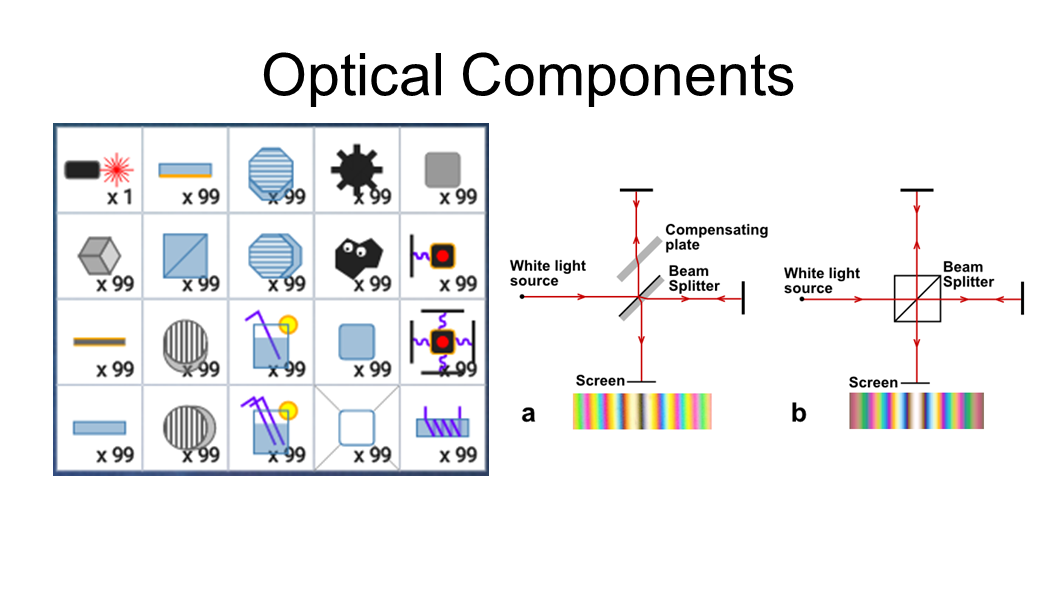 Quantum Game is a puzzle game based on photons
and their interactions. It models the amplitude,
phase, and polarization of a single photon as it
passes through optical filters, allowing it to split into
superpositions and interact with itself. The game
teaches the player about phase, polarization, and
interference through a series of puzzles.
Quantum Game is a puzzle game based on photons
and their interactions. It models the amplitude,
phase, and polarization of a single photon as it
passes through optical filters, allowing it to split into
superpositions and interact with itself. The game
teaches the player about phase, polarization, and
interference through a series of puzzles.
There are two versions of the game. The one I used
for this project is the beta version. As of this year,
there is a new, rewritten version being developed
with an updated user interface, but I found that it
didn’t work as well as the old version for my
purposes.
 The game uses many optical components found in
optical experiments, including mirrors, beam splitters,
quarter wave plates, and various polarizing filters.
The game uses many optical components found in
optical experiments, including mirrors, beam splitters,
quarter wave plates, and various polarizing filters.
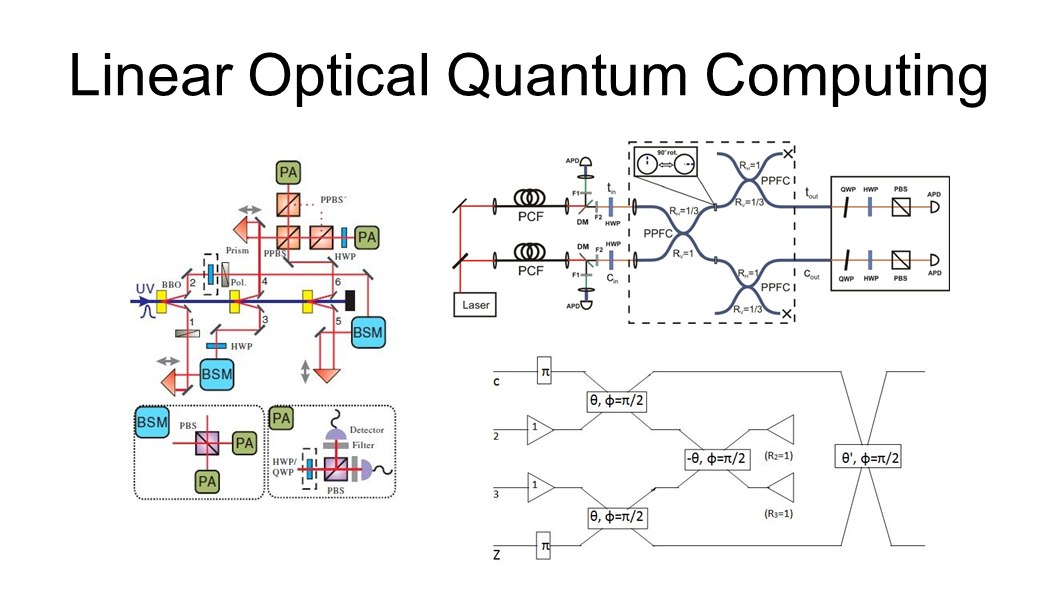
 There has been significant research into using these
optical components for quantum computing. The
optical components in Quantum Game are linear, so
it falls into the field of linear optical quantum
computing. I’ll discuss the consequences of this later
in the presentation.
There has been significant research into using these
optical components for quantum computing. The
optical components in Quantum Game are linear, so
it falls into the field of linear optical quantum
computing. I’ll discuss the consequences of this later
in the presentation.
 From my prior experience with this game’s sandbox
mode, I knew that I would need more space than the
13 by 10 grid it provides. This is where the
programming part of the project enters the picture.
From my prior experience with this game’s sandbox
mode, I knew that I would need more space than the
13 by 10 grid it provides. This is where the
programming part of the project enters the picture.
The game is written in JavaScript, including an
interface built with D3 and a custom tensor engine.
The engine works fine with an increased board size,
but the user interface does not move properly with
the board, for instance making it impossible to press
the Play button. I added some code to fix the UI
positioning. There are still some limitations with the
overall scale and the animation canvas, but I was
able to increase the board size to 32 by 16.
 My next task was to work out the math for the qubits. While
I’ve previously struggled to understand the math behind
this game, this time I had a better understanding of
matrices. There are multiple representations to use for a
logical qubit, but the one that I chose to understand the
gates is polarization and phase. I chose these two states
to be the |0> and |1> states.
My next task was to work out the math for the qubits. While
I’ve previously struggled to understand the math behind
this game, this time I had a better understanding of
matrices. There are multiple representations to use for a
logical qubit, but the one that I chose to understand the
gates is polarization and phase. I chose these two states
to be the |0> and |1> states.
One nice feature of this game is the encyclopedia, which
includes a representation of the matrix transformation for
each element. I found that the sugar solutions apply a Y
rotation with a phase shift. The quarter-wave plate is just a
phase shift, which is useful for counteracting the phase
shift of the other gates. A diagonal mirror is useful for
changing the direction and also happens to apply a Z gate.
The polarized quarter wave plates are useful for creating a
Z rotation without changing the direction.
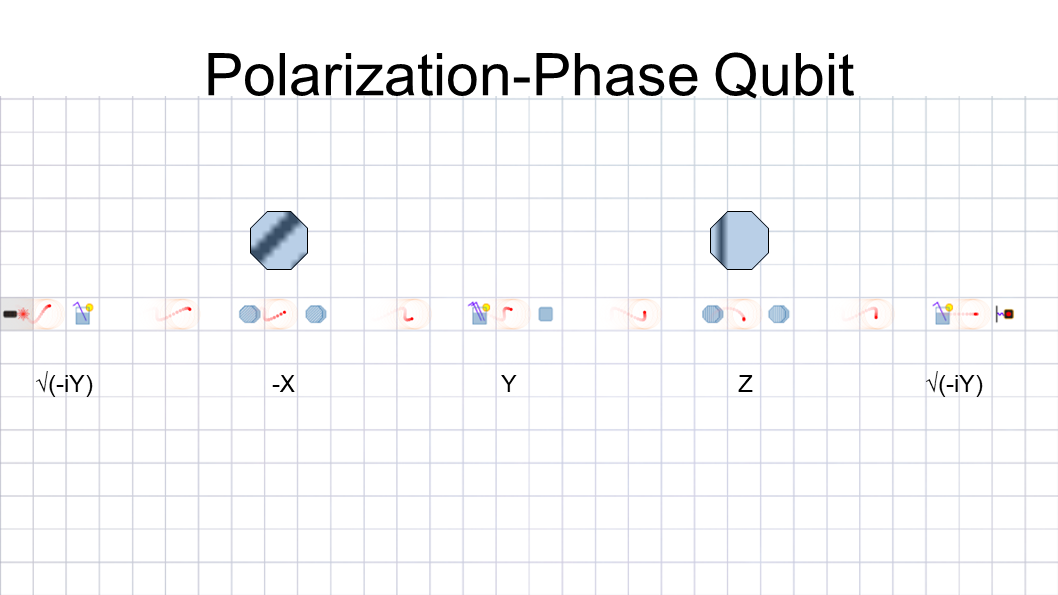 I attempted to recreate X, Y, and Z gates using three
different representations of logical qubits. I made
some mistakes with the phase here and there, so I’ll
point those out.
This first representation is the polarization-phase qubit,
which I used in the last slide. We can use a sugar
solution to perform a sqrt(Y) rotation with a phase
shift, giving us a superposition of |0> and |1> states
somewhat similar to a Hadamard gate. Next, we
perform a X gate using a diagonally polarized
quarter-wave plate, although I chose the wrong
diagonal so it adds a phase shift. Next, we use a
sugar solution and a quarter wave plate for a Y gate,
then a vertically polarized quarter-wave plate for a Z
gate. Finally, we use the same sugar solution as at
the start to move it back into the logical basis,
although with the phase shift, it ends up as a |1>.
I attempted to recreate X, Y, and Z gates using three
different representations of logical qubits. I made
some mistakes with the phase here and there, so I’ll
point those out.
This first representation is the polarization-phase qubit,
which I used in the last slide. We can use a sugar
solution to perform a sqrt(Y) rotation with a phase
shift, giving us a superposition of |0> and |1> states
somewhat similar to a Hadamard gate. Next, we
perform a X gate using a diagonally polarized
quarter-wave plate, although I chose the wrong
diagonal so it adds a phase shift. Next, we use a
sugar solution and a quarter wave plate for a Y gate,
then a vertically polarized quarter-wave plate for a Z
gate. Finally, we use the same sugar solution as at
the start to move it back into the logical basis,
although with the phase shift, it ends up as a |1>.
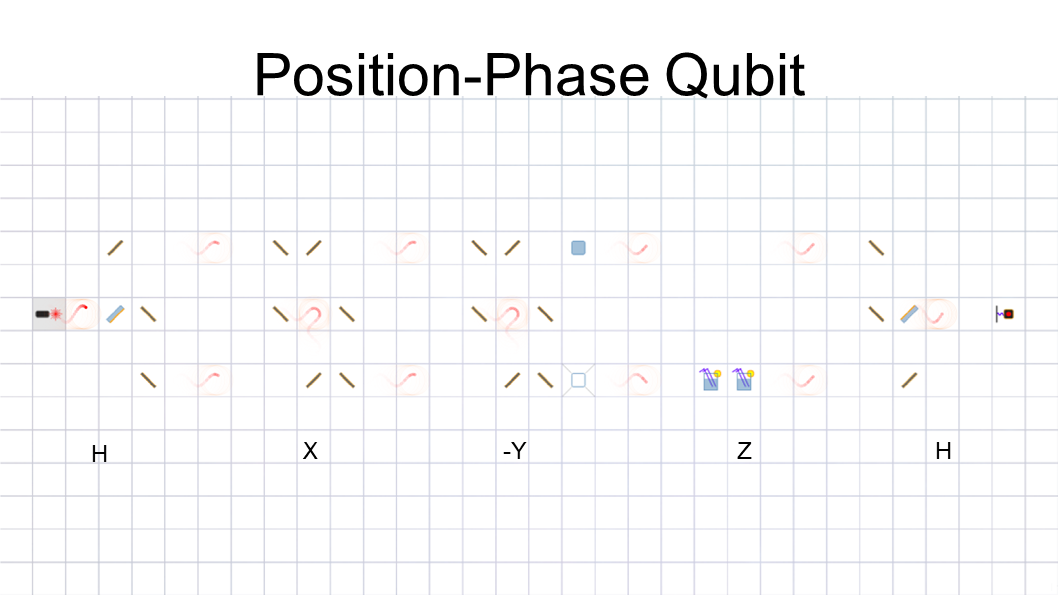 Next, we’ll look at the position-phase qubit. We apply
a true Hadamard gate this time using a coated beam
splitter and some mirrors. We perform an X gate by
simply swapping the positions with mirrors, which
has no effect on the |+> state. Then, we create a
negative Y gate using an X gate and some phase
shifting. If I had swapped the quarter-wave plate and
the vacuum jar, it would’ve been a positive Y gate.
The Z gate is simply a phase shift, which we perform
using two double sugar solutions instead of four
quarter-wave plates. Finally, we apply the Hadamard
gate again to get a logical |0> state with phase shift.
Next, we’ll look at the position-phase qubit. We apply
a true Hadamard gate this time using a coated beam
splitter and some mirrors. We perform an X gate by
simply swapping the positions with mirrors, which
has no effect on the |+> state. Then, we create a
negative Y gate using an X gate and some phase
shifting. If I had swapped the quarter-wave plate and
the vacuum jar, it would’ve been a positive Y gate.
The Z gate is simply a phase shift, which we perform
using two double sugar solutions instead of four
quarter-wave plates. Finally, we apply the Hadamard
gate again to get a logical |0> state with phase shift.
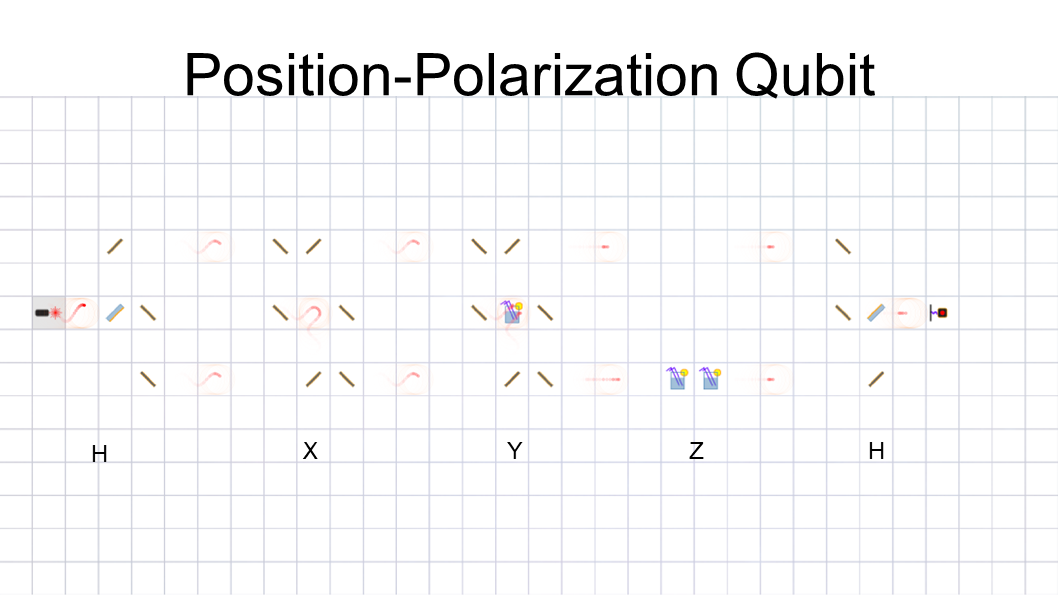 I also implemented a somewhat unconventional logical
qubit using position and polarization. The
polarization and phase are mathematically similar, so
I figured I’d give it a shot. This setup is similar to the
last one, except we use sugar solutions in place of
quarter-wave plates. For the Y gate, we can put the
sugar solution in the center since one of the qubits
has a temporary Z rotation from the mirrors. I may
have gotten this one right, but it’s hard to tell since
both phase and polarization can negate a qubit.
I also implemented a somewhat unconventional logical
qubit using position and polarization. The
polarization and phase are mathematically similar, so
I figured I’d give it a shot. This setup is similar to the
last one, except we use sugar solutions in place of
quarter-wave plates. For the Y gate, we can put the
sugar solution in the center since one of the qubits
has a temporary Z rotation from the mirrors. I may
have gotten this one right, but it’s hard to tell since
both phase and polarization can negate a qubit.
 We can convert between position and polarization
using a polarizing beam splitter. Here, we convert
between the polarization-phase and position-phase
representations, performing only Y and Z gates since
the X gate is a no-op on a |+> state and I didn’t give
myself enough room.
We can convert between position and polarization
using a polarizing beam splitter. Here, we convert
between the polarization-phase and position-phase
representations, performing only Y and Z gates since
the X gate is a no-op on a |+> state and I didn’t give
myself enough room.
 So far, we’ve been looking at rotations on one qubit.
One last interesting thing we can do with a single
qubit is demonstrate the basics of the BB84 protocol.
Alice wants to send a bit to Bob while preventing
Eve from intercepting it. Alice chooses either an
orthogonal or diagonal filter at random and polarizes
her photon in one of two directions accordingly. Bob
also chooses a filter at random and can detect the
encoded bit using two detectors and a polarizing
beam splitter. Alice and Bob compare filters after the
photon is received. If Alice and Bob choose the
same filter, Bob receives the bit. If they choose
different filters, Bob measures a random bit. If Eve
intercepts the photon, Bob detects no photon and
can notify Alice.
So far, we’ve been looking at rotations on one qubit.
One last interesting thing we can do with a single
qubit is demonstrate the basics of the BB84 protocol.
Alice wants to send a bit to Bob while preventing
Eve from intercepting it. Alice chooses either an
orthogonal or diagonal filter at random and polarizes
her photon in one of two directions accordingly. Bob
also chooses a filter at random and can detect the
encoded bit using two detectors and a polarizing
beam splitter. Alice and Bob compare filters after the
photon is received. If Alice and Bob choose the
same filter, Bob receives the bit. If they choose
different filters, Bob measures a random bit. If Eve
intercepts the photon, Bob detects no photon and
can notify Alice.
 But wait: didn’t I say there was a lot of research into linear
optical quantum computing? Indeed, there are several
research groups that have created CNOT gates using
linear optical components. However, these gates are not
perfect and have a probability of succeeding. All in all,
these approaches seemed to complicated to implement in
Quantum Game. Nevertheless, it would be an interesting
route to pursue further. The KLM scheme uses a quantum
teleportation trick to allow gates to be repeated until
success, which could be promising.
But wait: didn’t I say there was a lot of research into linear
optical quantum computing? Indeed, there are several
research groups that have created CNOT gates using
linear optical components. However, these gates are not
perfect and have a probability of succeeding. All in all,
these approaches seemed to complicated to implement in
Quantum Game. Nevertheless, it would be an interesting
route to pursue further. The KLM scheme uses a quantum
teleportation trick to allow gates to be repeated until
success, which could be promising.
It turns out the new version of the game may actually have
entanglement! There is a little bit of code in there for a
non-linear crystal, specifically a barium-borate crystal. The
crystal’s operation isn’t implemented yet, and it would have
to be modeled as an additional photon source, so it’ll
require further work before it’s available.
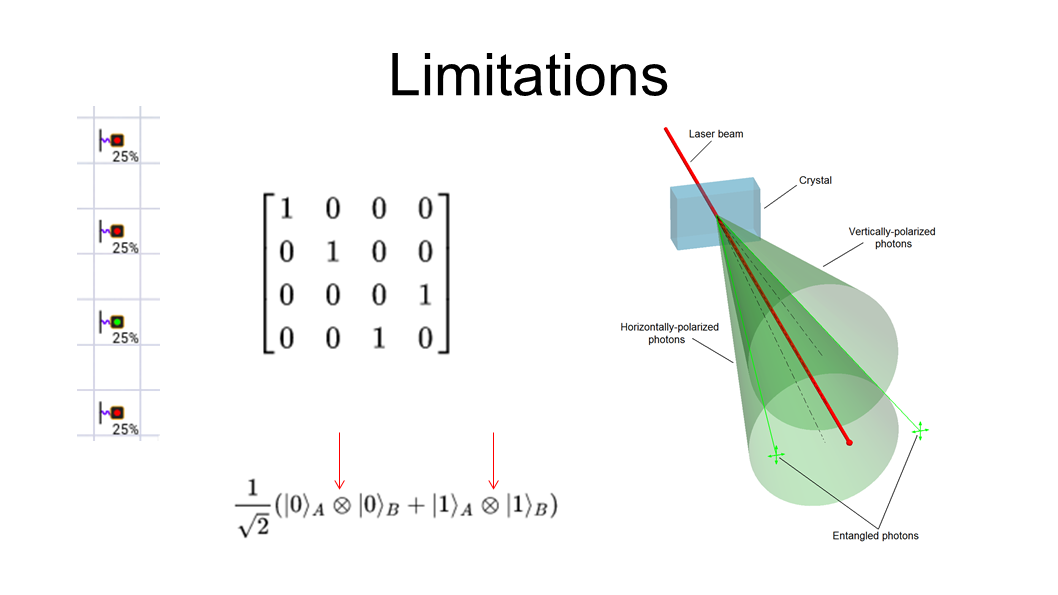 What about multiple qubits? Despite my efforts, I
couldn’t produce a meaningful interaction with two
qubits. In fact, I don’t think entanglement is possible
given the available optical filters. I can represent two
qubits as a four-state system, but this approach
would require an exponential amount of states for
more qubits. Also, there is only one photon to
measure, so if I wanted to measure two qubits, I’d
have to find a way to decompose them into four
states, effectively performing a Tensor product. I’m
pretty sure this is impossible because it’s a linear
optical system. Generally, entangled states are
produced by non-linear crystals, and I don’t have any
of those.
What about multiple qubits? Despite my efforts, I
couldn’t produce a meaningful interaction with two
qubits. In fact, I don’t think entanglement is possible
given the available optical filters. I can represent two
qubits as a four-state system, but this approach
would require an exponential amount of states for
more qubits. Also, there is only one photon to
measure, so if I wanted to measure two qubits, I’d
have to find a way to decompose them into four
states, effectively performing a Tensor product. I’m
pretty sure this is impossible because it’s a linear
optical system. Generally, entangled states are
produced by non-linear crystals, and I don’t have any
of those.
 Try it at https://turtle1331.github.io/quantum-game/bundled/
Thank you for your attention! Any questions?
Try it at https://turtle1331.github.io/quantum-game/bundled/
Thank you for your attention! Any questions?
Image Sources
Screenshots (edited) from:
https://avatars0.githubusercontent.com/u/60074853?s=200&v=4
https://upload.wikimedia.org/wikipedia/commons/2/20/Michelson_interferometer_using_white_light.png
https://phys.org/newman/gfx/news/hires/teleportationentanglinggate.jpg
https://www.researchgate.net/profile/Alex_Clark2/publication/1910759/figure/fig2/AS:279546147426322@1443660403856/An-all-optical-fibre-quantum-CNOT-gate-with-heralded-single-photon-sources-A-ps-708-nm.png
https://upload.wikimedia.org/wikipedia/commons/a/a4/NSCZGate.JPG
https://upload.wikimedia.org/wikipedia/commons/2/2d/SPDC_figure.png













